La Serie de Fibonacci y su utilización

Una de las herramientas más útiles que podemos utilizar en nuestro análisis gráfico del mercado, son los números de Fibonacci. ¿De dónde viene?

Introducción

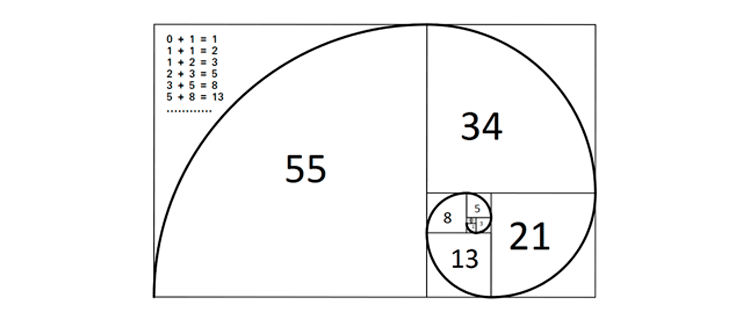
Leonardo Pisano Bogollo (1170-1250) fue un matemático italiano originario de Pisa. Se cree que este matemático fue el primero en presentar una serie matemática en el mundo occidental, que se construía de la siguiente manera “comenzando con 0 y 1, a partir de este momento sumamos los dos números anteriores y así obtenemos el siguiente:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ….

Es decir,
0,1, (0+1) =1, (1+1) = 2, (1+2) = 3, (3+5) =8, (5+8) =13, (13+21) =34, etc.

Esta serie se extiende hacia el infinito. Pero lo más llamativo de esta serie reside en las relaciones existentes entre los números que la componen. Ya que dan lugar a lo que llamamos los porcentajes de corrección de Fibonacci y en especial al Ratio de Oro.

Relaciones Especiales y el Ratio de ORO

Para formarlos basta con realizar las siguientes operaciones:

Si dividimos números consecutivos de la serie entre si, poniendo en el numerador el más bajo de los dos, descubrimos que el resultado tiende a una cifra exacta, 0.6180:
…(8/13)=0.615, (13/21)=0.619, (21/34)=0.6176, (34/55)=0.6181, (55/89)= 0.6179 …. de esta relación entre los números de la serie nace el 61.8% de corrección de Fibonacci.

Si dividimos números NO consecutivos de la serie entre sí, poniendo en el numerador el más bajo de los dos, descubrimos que el resultado tiende a una cifra exacta, 0.3820:
…(8/21)=0,3809, (13/34)=0.3820, (21/55)=0.3818, (34/89)=0.3820, (55/144)= 0.3819 …. de esta relación entre los números de la serie nace el 38,2% de corrección de Fibonacci.

Existen otras relaciones curiosas, como que 1 – 0.618 = 0.382. O que el cociente de cada tres números de separación en la serie da un resultado que tiende a 23.6% (primer número de corrección de Fibonacci). Pero sin duda alguna una de las propiedades más importantes de la serie es la siguiente:

Si dividimos números consecutivos de la serie entre sí, poniendo en el numerador el más alto de los dos, descubrimos que el resultado tiende a una cifra exacta, 1.6180:
…(13/8)=1.625, (21/13)=1.6153, (34/21)=1.6190, (55/34)=1.6176, (89/55)= 1.6181 …. a medida que avanzamos en las operaciones dentro de la serie el resultado tiende a 1.6180.

Se denomina a 1.6180 como el Ratio de Oro

El inverso de 1.618 es 0.618. Estos ratios se encuentran presentes en la naturaleza, la arquitectura, el arte y la biología, entre otras ramas. Y no solo de una manera intencionada sino de forma natural. De esta forma, vemos que están presentes en construcciones famosas como el Partenón, las pirámides, pero también en elementos de la naturaleza donde el hombre no ha tenido ninguna influencia, como en las hojas de las flores, en la espiral de las conchas marinas, en la espiral de la Vía Láctea y de otras Galaxias. Por tanto, estamos ante unos números que reflejan cierto equilibrio natural, que tienen efecto en muy diversas facetas del universo. A partir de ahí, algunos estudiosos de los comportamientos de los mercados financieros, como Ralph Nelson Elliot (1871–1948), los incorporaron a su teoría de las Ondas de Elliot, describiendo las pautas de comportamiento en los ciclos alcistas y bajistas.

Porcentajes de Corrección

Las correcciones más comunes son el 23.6%, el 38.2%, el 50% y el 61.80%. Todos estos números se originan, como ya hemos visto, en las relaciones existentes entre los números de la serie de Fibonacci, excepto el 50% que viene de la Teoría de Dow, donde una de las premisas dice, “que los índices cuando comienzan un movimiento de vuelta tienden a corregir la mitad de los movimientos impulsivos previos”.

• La corrección del 23.6% es pequeña, y suele darse solo en breves “pullbacks” o en estructuras correctivas menores como las “banderas”.
• La corrección del 38.2% y el 50% se considerada moderada, y veremos que se produce con mucha frecuencia.
• La corrección del 61.8% a veces se denomina la “corrección de oro” y suele representar la corrección máxima razonable antes de que el mercado cambie la tendencia definitivamente.

Como utilizar los porcentajes de corrección

Como en casi todas las herramientas de análisis, hay un enfoque subjetivo en la manera de aplicar estos criterios. Pero sin duda alguna, cuando combinamos la fuerza de los niveles de corrección, junto a otro tipo de análisis técnico, es cuando mejoramos realmente la eficiencia de las señales. De este modo, si un área de corrección de Fibonacci coincide con un nivel de soporte o resistencia, resulta más fiable. La coincidencia de áreas de corrección de Fibonacci, con señales de en los indicadores técnicos, también ayuda a validar posibles rebotes en dichos puntos. Por último, existen las áreas de confluencia formadas por el análisis simultaneo de una tendencia principal y una tendencia secundaria que forma parte de la principal. En ocasiones vemos como el porcentaje de corrección menor sobre la tendencia estructural coincide con un porcentaje mayor de la tendencia reciente. En ese caso se forma lo que denominamos área de confluencia, y el soporte o la resistencia que ofrecen es mucho más significativo. Veamos algunos ejemplos:

 

Corrección del 61.8% en el Euro vs Australiano

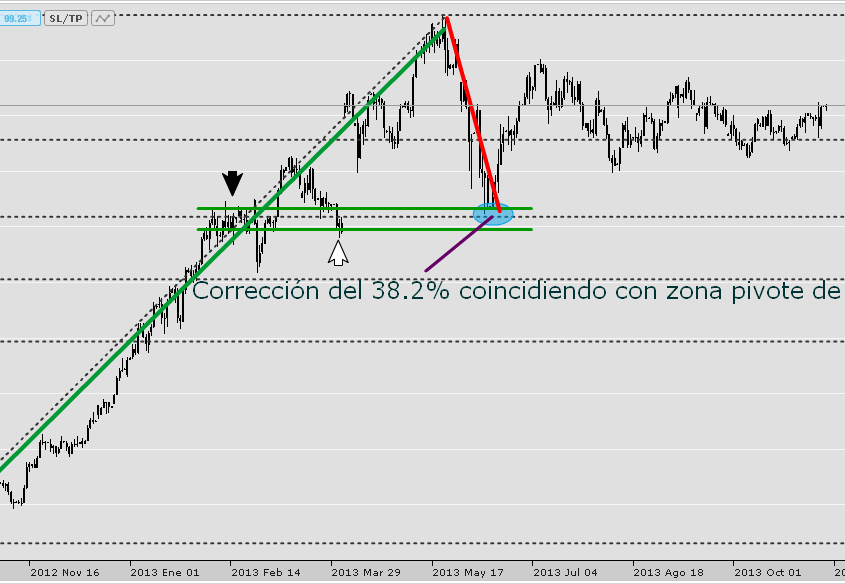
Corrección del 38.2% del Dólar – Yen

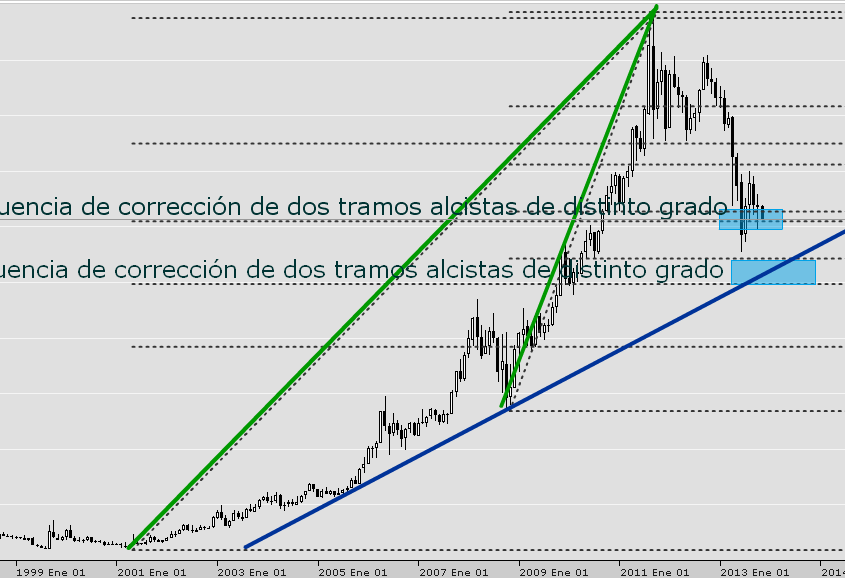
Áreas de Confluencia en el Oro a nivel mensual.